The Importance of Remainders!

 Can you answer this? 🤔

4L & 9L

How?

Fill the 9L bottle.

Fill the 4L bottle using the water you filled in the 9L bottle.

By doing this, you now have 5L remaining in the 9L bottle. (9L - 4L)

Now empty out the 4L bottle.

Fill the 4L bottle up with water again using the water you have remaining in the 9L bottle (that is, 5L of water)

By doing this, you now have 1L remaining in the 9L bottle. (5L - 4L)

In other words,

Fill up the 9L bottle. Empty the water into the 4L bottle, twice. You have 1L left.

The importance of remainders!

Peasant Multiplication

Have you ever heard of what Peasant Multiplication is?

SPOILER: It has something to do with multiplication...

Peasant Multiplication (A.K.A. Russian peasant Multiplication) is a method of multiplying two numbers that was rediscovered in Russia during the 19th century, and was popularly used among uneducated peasants for daily practicality.

It is similar to Egyptian multiplication.

However, its foundational concepts developed in the work of late German mathematician Gottfried Wilhelm Leibniz (1600s). 

Today, we know this as converting ordinary base 10 multiplication into base 2 (binary) multiplication. This is essential to computing because it makes the task easier for the computer to process!

How does it work?

Let’s try an example together! Here’s something we all know:

What is 40 x 10?

That's right, it's 400.

Now let’s see how we can get this answer using Peasant Multiplication!

Step 1 - FORMAT

Arrange the 2 numbers on the top of a T-table. 

*Note: For multiplying more than two numbers (say three numbers), you would create a T-table to find the product of two numbers first, then create another T-table with the product you got and the third number to get your final answer.*

Step 2 - DECIDE

It doesn’t matter which number you pick to halve, just make sure you double the other. 

(I’ll show you this works either way afterwards...)

Step 3 - COMMIT!

After you decide, you must continue doing that operation for the rest of that column. 

We continue this process, each time halving or doubling the previous number in its column to get the next until we get stuck with an odd number. 

Step 4 - KEEP IT EVEN!

When this happens, we just write the even number (the number in the doubling column) of that row next to the table and save for later. 

Step 5 - CONTINUE!

When we continue the process, we divide the odd number by 2 just like before but  only write the quotient  and dispose the remainder. 

5 ÷ 2 = 2.5 or 2R1; only write the quotient, (2)

Step 6 - FINAL STOP!

Eventually we will get a quotient of 1 on the halving side. Since 1 is also an odd number, we simply write even number next to it.

Step 7 - ADD

It works the other way too!!

Tip: it’s actually much faster when you choose to halve the already smaller number.

Why does it work? 

We can see that as we went down each column simultaneously, as long as the previous number in the halving column is even, the row that follows it would have the same product as the original question.

In other words, the multiplication of the two numbers in that row would yield the same exact product. Example, 40 x 10 = 400 = 80 x 5.

When a number in the halving column is odd, the product of the row that follows is less than the product because we got rid of the remainder.

Example, 40 x 10 = 400 = 160 x 2 + N,  where “N” represents the missing value to make the equation true. 

To find N we use simple algebra:

40 x 100 = 400 = 320 + 80, N = 80. Notice how we already wrote out the 80.

And so we now know that the rest of the rows’ products (regardless of the odd/even nature of halving column) would be lacking at least 80 to equal 400. 

The next time an odd number appears in the halving column, its corresponding even number would be added the the product of the next row. 

Works if we halve the 40 side too...

40 in binary is 101000.

(1 x 320) + (0 x 160) + (1 x 80) + (0 x 40) + (0 x 20) + (0 x 10)

Again, this is just (1 x 320) + (1 x 80) = 400.

Thank you for reading; I hoped you learned something new. I’m open to questions if you have any! 😊

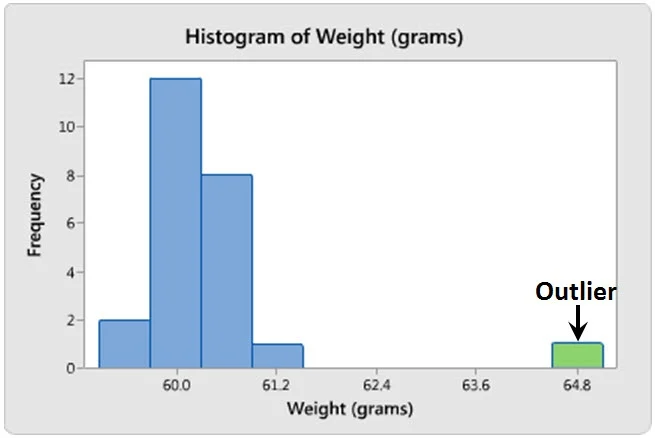
AP Statistics - Possible Data Histograms

 Normal Distribution (A.K.A. the Bell Curve):

Skewed Right Distribution:

Skewed Left Distribution:

Graphs may follow a slight variation (for example, a graph may begin to follow a skewed right distribution but then start to have outliers). We usually analyze the overall shape the graph tends to follow. 

Outliers: data that does not align with the general pattern of distribution... this data is considered inconsistent.

Revisiting - Precise and Accurate data

Accurate: When data is accurate, the data collected is very close to the real value. However, the data does not have to be totally precise. For example, the measurement of mass in grams for the same item is always exactly or slightly off from the real measurement value. Comparing data to a reference point.

Precise: When data is precise, the data collected is very close to each other (constantly consistent). This does not necessarily mean, however, that the data is accurate. For example, measurements of mass in grams for the same item can vary, but remains precise when all measurement values are very close to each other (less variation). Comparing individual data to overall data.

Cool!

Supplemental Topics, Branching out more with Calculus l

Chapter 8: Supplemental Topics:

 

Identifying the graphs of f(x), f’(x) and f’’(x).

When examining the graph of f(x) to find f’(x) and examining the graph of f’(x) to find f’’(x):

• Does the function’s curve move downwards (decreasing) going right from that point to its rightmost point (in which case the slope (y-value of the derivative) would be negative) or does the curve go upwards (increasing) from that point to the rightmost point (in which case the slope (y-value of the derivative) would be positive). 

• The steeper the slope is, the greater the absolute value of the y-value of the derivative function will be. 

Limits (L’Hopital’s Rule) and Related Rates:

When we are relating the rate of two functions f(x) and g(x), we consider the following:

For indeterminate forms, recall L’Hopital’s Rule. 

L'Hopital's Rule: derive the numerator and denominator (keep it in fractional form), then plug in the value the limit approaches. If after plugging in the value, you come back to the original limit, try the rule again. If it happens to be in the exact same form again, that means that there may be no proper conclusion. 

Reaching back to F.T.O.C. and exploring the graphs of F(x), and F’(x).

Since F is just a function that refers to the area under the curve f(x), we look at the behavior of the area under the curve when we are examining F. 

Area above the x-axis within an interval is considered a positive area. F(x) is a y-value = the area from a starting point of “a” to “x”. If the area remains positive from “a” to “x”, and “x” is the x-value at which f(x) = 0, (assuming the function’s next rightmost point from “x” would be a negative y-value), then we know the area is getting bigger in value from “a” towards “x” and getting more positive and when it gets to “x”, it is at its max. 

Area below the x-axis within an interval is considered a negative area. If the area remains negative from “a” to “x”, and “x” is the x-value at which f(x) = 0, (assuming the function’s next rightmost point from “x” would be a positive y-value), then we know the area is getting smaller in value from “a” towards “x” and getting more negative and when it gets to x, it is at its min. 

Taking the derivative of F, or F’(x) we get our original curve f(x):

Discrete data: just data points, or points that don’t necessarily follow a function/ graph. 

Put them on a graph to help with visualization! This will also help with estimating different types of area. Make sure you know what the area really implies, so that you can put correct units! Find what f(t)’s units are and dt’s units are and multiply them to find the units of the area. 

Recall the ways to approximate area:

• Left/Right areas 

• Trapezoid method

• Simpson’s method

*** To find minimum and maximum units of area, use the left/right sums (identify which gives underestimates and which overestimates).***

Averages:

Velocity from any (d1, t1) to (d2, t2) = change in distance (d2 - d1) / change in time (t2 - t1)

Average velocity = change in total distance (d(t) - d(0)) / change in total time (t - 0), where “t” represents the last time value. 

Acceleration from any (v1, t1) to (v2, t2) = change in velocity (v2 - v1) / change in time (t2 - t1)

Average acceleration = change in total velocity (v(t) - v(0)) / change in total time (t - 0), where “t” represents the last time value. 

Average of value of a function:

Recall…

.

Calculus l - Differential Equations

Differential equations: Equations that involve derivatives. The solution to a differential equation is not a set of values, but a function or set of functions. 

Methods to solve:

Separation of Variables method: Only works if variables are isolatable. 

Step 1.) Get all like variables on the same side. For example, all the x’s on one side, and all the y’s on the other. 

Step 2.) Integrate! (After you integrate, you’ll get a “+ C” on both sides, just join the “+ C”’s into one “+ C” on the side of the independent variable (the variable you are integrating with respect to, most commonly known as x)).

Step 4.) Isolate the dependent variable if not yet done (most commonly known as y).

Step 5.) (This step depends, you can also do this step before step 4) If you are given an initial condition, say y(1) = 2, then you can plug in 1 for x and 2 for y to solve for c. This will help us find a general equation. 

To check if a function satisfies the differential equation, we can plug it in for “y” and check. 

Tips: 

Whenever we have something multiplied by/divided by/raised to the base of/ exponent raised to the base of our constant “C”, we just convert that entire term into a “+ C”. If something is multiplied to a constant it is still just some constant.

 

If we have more than one “+ C”, then we can combine them into one “+ C” and just put it on one side.

To cancel a natural log, we can raise both sides to a base e. To cancel an absolute value, we can just write the plus or minus value of the other side. 

Growth V.S. Decay

Growth differential equation:

The actual function used to find solutions (found by separation of variables method on growth differential):

r is just k. 

Decay differential equation:

r is just k.

Actual function used to find solutions (found by separation of variables method on decay differential):

,  k is just the negative natural log of the percent decay in decimal over the time it takes for that percentage of decay. 

Newton’s Law of Cooling

Used to answer “How long until you get the desired temperature?”. Questions relating time and temperature. 

Differential equation:

*For Newton's law of cooling, if k is not given, assume a good approximation would be 0.0005.*

Slope fields: a bunch of small dashes on points that exist on a graph that represent the slope of the function at certain points. These dashes represent the derivative of a point on the graph, but extend outwards both sides to form an actual dash or line. They are used to approximate the slope with the help of delta x. Delta x will tell the distance from one x-value to another, to approximate the slope you would connect following the path of the dashes that exist at these x-values on the graph. To better the approximation, make delta x a smaller number. 

Linearization

Local Linear Approximation or “Linearization” of f(x) at the point x = a.

y = f(a) + f’(a)(x-a)

Newton’s Method (may not work in all cases, for example, if you pick an x-value that has a y min or max, then the tangent line will have a slope of zero which is just a horizontal line that will never intersect the x-axis again and hence, won’t get you the next x-value for approximation). 

Steps to solve:

Step 1.) Get a rough sketch of the graph and identify the x-value that’s closest to the zero. Avoid picking an x-value that you know will give a max or min y-value. The x-value you pick will be your x1, (A.K.A your first guess).

Step 2.) Using the formula above, original function, function’s derivative, and x1, you can plug in x1 for xn and solve for xn+1 or x1+1 which is just x2. Repeat the process, each time replacing the xn with the value you obtained from the previous calculation, and incrementing n up by 1. For example, in the next incrementation, you would plug in the x2 that you found using the formula the first time for xn and solve for x2+1 or x3. 

Step 3.) Depending on “to __ places of accuracy”, (say, for example, 4 places of accuracy), you would keep repeating the process until you notice that the value you obtained from the previous calculation has the exact same number(s) in the same place value position as the calculation you just did.

For example x3 = 2.35443 and x4 = 2.30284. Notice how x3 and x4 seem to settle on the first two values being 2.3. Continue this process until you know for sure up to, in this example, 4 decimal places. 

The Trapezoid Rule is essentially the average of the left and right areas: 

b and a are the bounds, n is the number of intervals.

The Simpson’s Rule (most accurate approximation):

b and a are the bounds, n is the number of intervals.