Calculus l - Applications of Integration

Applications of Integration

Area:

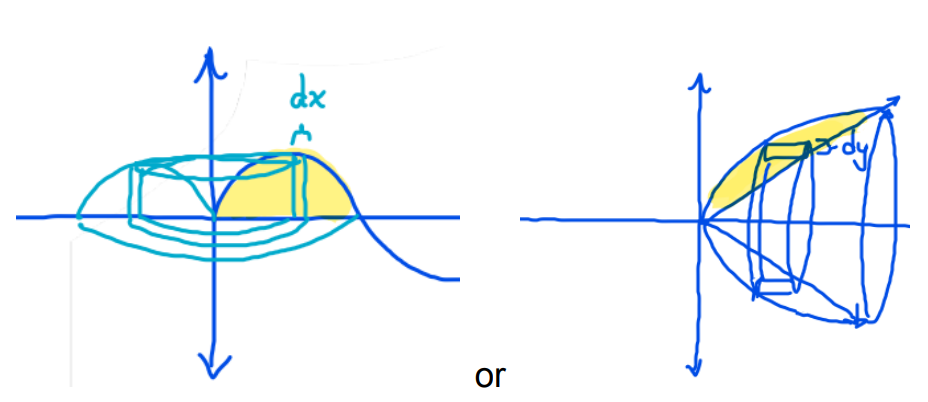
Integrating using rectangles with horizontal heights:

Since the height is horizontal (parallel to the x-axis), the width must be vertical (parallel to the y-axis). The width will be a small change in y, or “dy”. This implies we are integrating with respect to y. Generally speaking, the height of a rectangle will be the right x-value minus the left x-value. Our right x-values will come from the rightmost function, and our left x-values will come from the leftmost function. When we integrate with respect to y, however, we need everything inside the integral to be in terms of y. So, we would inverse the functions.

Then we set up a definite integral because we are going to be summing up multiple of these small rectangle areas. The bound, if not specified, can be found by setting both functions to equal and finding intersection points (the y-values of those points that is).

Integrating using rectangles with vertical heights:

Since the height is vertical (parallel to the y-axis), the width must be horizontal (parallel to the x-axis). The width will be a small change in x, or “dx”. This implies we are integrating with respect to x. Generally speaking, the height of a rectangle will be the top y-value minus the bottom y-value. Our top y-values will come from the uppermost function, and our bottom y-values will come from the bottommost function. Make sure everything is in terms of x inside the integral!

Then we set up a definite integral because we are going to be summing up multiple of these small rectangle areas. The bound, if not specified, can be found by setting both functions to equal and finding intersection points (the x-values of those points that is).

Volume

Using disk/ washer method:

1. Get a sketch, it’ll help with visualization.
2. Identify the bounded area using the functions provided.
3. Rotate that area about the axis of rotation (given).

• If the axis of rotation is parallel to the y-axis, then you will be integrating with respect to y.
• If the axis of rotation is parallel to the x-axis, then you will be integrating with respect to x.
• 
  

Recall this example for visualization:

4. Create a cross section by slicing the solid perpendicular to the axis of rotation. Identify whether it is a washer or disk. (Usually, if the area is bounded between a function and the axis of rotation, it will be a disk. Conversely, if the area is bounded between functions that don’t include the axis of rotation, the result will be a washer. There are also scenarios, however, where the axis of rotation is a bound but only partially bounds a side, in cases like these, you would need to set up two different integrals to get optimal results. This is because there are two different functions that make up that side of the area on separate bounds).
5. 
   
6. Identify the area of the face of the cross section.
7. 
   

• For washers:  pi * R^2 - pi * r^2, where “R” is the bigger radius, and “r” is the smaller radius.
• For disks:  pi * r^2
• 
  

Radius is determined by the function responsible for its change. The radius is the distance from a point on that function to the axis of rotation. The function that’s uppermost would yield a greater distance from the axis of rotation and, in turn, have a larger radius (R).

6. Last, set up an integral. The bounds, if not specified, are the outermost intersection points. Make sure to rewrite any functions in terms of whichever variable you’re integrating with respect to. Also, you can factor out a pi in washers, and then take it out of the integral or just take the pi out of the integral for disks, to look condensed like this example of integrating with respect to x:
7. 
   
8. 

Then, solve it!

Volume using shells:

If the method above doesn’t work, use the shell method… You can use the shell method when you notice that the outer function responsible for the bigger radius is the exact same function responsible for the smaller radius.

Use the formula: (circumference)(height)(thickness)

1. Follow steps from Volume using disk/ washer method up until 2.
2. Rotate the area about the axis of rotation
3. This time, instead of imagining rectangles perpendicular to the axis of rotation, our rectangles will be parallel to the axis of rotation. Connect two rectangles on opposite sides by following the path of the 3D solid. It should form a cylindrical shape:

4. When we unravel this cylinder, we will just end up getting a long rectangular box
5. 

Notice how the dimensions relate to the graph:

• Radius: see what the radius depends on.

In the first example from step 3, the radius depends on the distance from a point on sin x to the y-axis. Therefore, radius for is (the outermost function - the axis of rotation) which is (sin x - 0) or just sin x.

In the second example, the radius seems to depend on the distance from a y-value to the axis of rotation. Since both functions are continuous, both will yield the same y-value at different x-values. The distance between these x-values would be the height. Since dy is getting infinitely smaller, the position of the lengths will come increasingly closer to approach a single y-value, which is used to calculate the radius.

• Height: see what the height depends on.

In the first example, the height seems to correspond with the value of y at an x-value for sin x.

In the second example, the height is the difference between the right x-value (given by the rightmost function) and the left x-value (given by the leftmost function).

• Thickness:

Is always either dx or dy. Depends on whether the axis of rotation is parallel to the y-axis (in which case it would be dx) or parallel to the x-axis (in which case it would be dy).

First example: dx

Second example: dy

5. Set up the definite integral!

For anything else, always remember that the formula for volume is just the area of the face of a cross section multiplied by the thickness (or change in x or y). Once you find the volume for one cross section, just use a definite integral!

Work:

Hooke’s Law (springs): F = kx (Force is equal to spring constant multiplied by object’s displacement)

Basic work formula that only works when force is constant: W = Fd (Work is equal to force multiplied by displacement).

F = ma (Mass multiplied by acceleration) but acceleration in the y direction is just gravitational acceleration (9.8 m/ sec^2 only used in the metric system).

Force is also known as the weight. The work done by a variable force is the definite integral from a to b of the force function multiplied by dx.

Force isn’t constant when it requires increasing or decreasing force to lift/ drop a part of something throughout the process of work.

Units of Work, Force, and Distance:

Term	SI (metric system)	Imperial
Work	J (Joules)	Cal (Calories)
Force	N (newtons)	lb (pounds)
Distance	m (meters)	ft (feet)

 

Work required to lift/move/stretch something:

Identify how much force is required to lift/move a small amount of that thing (called dx or dy). Next, find a ratio that could relate two variables, for example, the force it takes to move an object a certain distance (you can use the spring constant here if you’re dealing with springs) and make a unit rate. Generally state the displacement from the small floating/suspended amount to the final destination as a value of x (for horizontal displacement) or y (for vertical displacement). Arrange these into a definite integral.

Work required to pump something:

Draw a diagram of the container of liquid and label the dimensions of it including the dimensions of the liquid in it. Your goal is to find how much work is required so that the liquid will come out of the container (reach the top).

Use the formula:

W = (density of liquid)*(gravitational acceleration)(definite integral from a to b)(volume of a cross section as a function of x)*(displacement) dx

Density = mass/ volume

Average value theorem:

If the function is continuous within an interval, then the function’s average value within that interval will exist as an y-value somewhere on the function in the interval. This is the formula for the average value of f(x).

Position, velocity, acceleration relations: